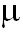Fracciones propias

Son las que son menores que 1 entero (están entre 0 y 1).

Ejemplo:

1 entero = toda la pizza

La pizza está cortada en 8 porciones. En cada plato hay 1 porción, por lo tanto en cada plato hay 1/8 de pizza.

1 ------> numerador
8 -----> denominador

En la bandeja quedaron 6 porciones, entonces en la bandeja hay 6/8 lo cual es lo mismo que 3/4.

Para saber si una fracción es propia o no, tengo que comparar el numerador con el denominador. Si el numerador es menor que el denominador, significa que tengo menos partes que un entero, entonces es menor que un entero y por lo tanto es propia.

En el dibujo: una porción de pizza es menos que una pizza entera. La fracción es 1/8; 1 es menor que 8 por eso es propia. 6 también es menor que 8 por lo tanto 6/8 es propia. Para tener 1 entero tengo que tener las 8 porciones en las cuales partí la pizza; siempre que tenga menos de 8 porciones voy a tener menos que un entero (menos que una pizza entera).

Fracciones impropias

Son las que son mayores que un entero.

Ejemplo
:

Tengo 1 alfajor y medio. Como tengo más que 1 entero (más que 1 alfajor entero) la fracción es impropia.

Por lo tanto tengo 1 entero y ½

1 entero = 2/2
entonces tengo en total 3/2 de alfajor

3 es mayor que 2 por eso es propia.

Fracciones aparentes

Son las que significan una cantidad exacta de enteros. Ejemplo:

Tengo 1 empanada entera y otra empanada partida en 2 pedazos. Cada pedazo es ½ de empanada. Si tengo 2 pedazos tengo 2/2 de empanada, lo cual es igual de grande que tener 1 empanada entera (2/2 es lo mismo que un entero).

Por lo tanto 2/2 = 1

Por eso 2/2 es una fracción aparente.

Si tengo 3 chocolates y cada uno está dividido en 6 pedazos, en total tengo 18 pedazos:

6 . 3 = 18

Cada pedazo es 1/6. Así que tengo 18/6.

Por lo tanto tener 3 chocolates es lo mismo que tener 18/6 de chocolates. O sea que 3 enteros es lo mismo que 18/6.

3 = 18/6

Por lo tanto 18/6 es una fracción aparente.

Comparación de fracciones

Obsérvese que a igual denominador y distinto numerador, la fracción más grande es la que tiene mayor numerador, porque es cuando tengo más partes. Ejemplos:

1/8 es menor que 3/8 y 3/8 es menor que 5/8 porque 1 es menor que 3 y 3 es menor que 5.

En cambio a igual numerador, la fracción es mayor cuanto menor sea el denominador, porque es cuando las partes son más grandes. Ejemplos:

Denominador común

La obtención del denominador común entre 2 fracciones se basa en la siguiente fórmula:

a . b/b = a

Esto se debe a que todo número dividido por sí mismo da 1:

b/b= 1

Entonces:

a . b/b = a . 1

Todo número multiplicado por 1 da ese mismo número:

a . 1 = a

Por eso multiplicar y dividir a cierto número por el mismo número (al número “a” lo multiplico por “b” y después lo divido por “b”) da el mismo número que tenía antes (vuelve a dar “a”).

Basándonos en ese concepto podemos, por empezar, sumar a números enteros con fracciones:

a/b + c = a/b + c . 1 = a/b + c . b/b = (a + c.b)/b

Ejemplo:

3/5 + 2 = 3/5 + 2.1 = 3/5 + 2.5/5 = (3 + 2.5)/5 = (3 + 10)/5 = 13/5

Con el mismo criterio podemos sumar 2 fracciones de denominadores diferentes:

a/b + c/d = (a/b).(d/d) + (c/d).(b/b) = (a.d + c.b)/(b.d)

(Recordar que b . d = d . b)

Ejemplo:

2/3 + 3/4 = (2/3).(4/4) + (3/4).(3/3) = (2.4 + 3.3)/(4.3) = (8+9)/12 = 17/12

A veces es más conveniente factorizar los denominadores antes de obtener el denominador común. Por ejemplo:

Supongamos que b = d . e

Entonces:

a/b + c/d = a/(d.e) + c/d = a/(d.e) + (c/d).(e/e) = (a + c.e)/(d.e)

Ejemplo:

1/2 + 1/6 = 1/2 + 1/(2.3) = (1/2).(3/3) + 1/(2.3) = (3 + 1)/(2.3) = 4/(2.3) =

= (2.2)/(2.3) = 2/3

(En el último paso factorizamos la fracción para simplificarla hasta su fracción irreducible)

También sucede que el Mínimo Común Múltiplo no necesariamente es multiplicar los 2 denominadores entre sí, aunque no sean uno múltiplo del otro. Para darse cuenta de esto también conviene factorizar. Supongamos que:

b = e . f

d = e . g

Entonces:

a/b + cd = a/(e.f) + c/(e.g) = (a/(e.f)).(g/g) + (c/(e.g)).(f/f) = (a.g + c.f)/(e.g.f)

Ejemplo:

1/6 + 2/15 = 1/(3.2) + 2/(3.5) = (1/(3.2)).(5/5) + (2/(3.5)).(2/2) =

= (5+4)/(3.5.2) = 9/(3.5.2) = (3.3)/(3.5.2) = 3/(5.2) = 3/10

(En el último paso también factorizamos)

Hibridización de orbitales

sp³

El carbono tiene CEE = 2s² 2p² en su estado fundamental. En su estado excitado un electrón s salta al nivel p y queda CEE = 2s¹ 2p³. Para formar los 4 enlaces simples (todos s) que necesita para alcanzar el octeto, debe conseguir que los 4 enlaces tengan la misma distancia y energía de enlace y que los ángulos de todos con todos sean los mismos. Para conseguir esto necesita que los orbitales sean iguales. Entonces se hibridizan en un tipo de orbital intermedio entre el s y el p, denominado sp³ porque tiene 1 electrón s y 3 electrones p (25% s, 75% p).

Esto es lo que ocurre con todos los enlaces simples de los elementos que cumplen con el octeto. Por ejemplo el oxígeno tiene CEE = 2s² 2p⁴ en su estado fundamental, lo cual implica que tiene 2 pares de electrones libres (que son 2 orbitales) y 2 electrones que formarán enlace (cada enlace será otro orbital), así que tiene en total 4 orbitales. Un par de electrones libres será un orbital s, el otro será un orbital p y los 2 electrones que forman enlace serán del orbital p. Para equiparar las distancias y energías de enlace estos 4 orbitales se hibridizan dando sp³. Esta es la hibridización que tendrá el oxígeno dentro del agua, dado que el agua consta de 2 enlaces simples.

sp²

Cuando el carbono forma un enlace doble, tiene 3 enlaces s y uno p (el enlace doble consta de un enlace s y uno p). El enlace p está formado por un orbital p puro (sin hibridizar). Los otros 3 orbitales son los que se van a hibridizar. Entonces tenemos 2 electrones p y uno s, por ende es sp² (1/3 s y 2/3 p).

Esto ocurre con todos los enlaces dobles de los elementos que cumplen con el octeto. Por ejemplo, el oxígeno puede utilizar uno de sus orbitales p para formar un enlace p, y quedan otros 3 orbitales que son: un par de electrones libres del orbital s, un par de electrones libres del orbital p y otro electrón del orbital p que también formará enlace. Entonces tenemos un orbital s y 2 orbitales p, que se hibridizan dando sp². Esta es la hibridización del oxígeno gaseoso, que consta de una unión doble (un enlace s y uno p).

También ocurre con los enlaces simples de algunos elementos que no cumplen con el octeto, por ejemplo: el boro. El boro tiene CEE = 2s² 2p¹ en su estado fundamental, y en su estado excitado pasa a ser CEE = 2s¹ 2p². Por lo tanto tiene 2 electrones p y uno s, con los cuales hace 3 orbitales sp² y formará un enlace simple con cada uno de ellos, resultando por ejemplo BF₃, ubicándose en una geometría triangular que es muy estable (la geometría es lo que determina que no cumpla con el octeto). Nótese que el carbono con el enlace doble también resulta dar una geometría triangular.

sp

Cuando el carbono forma algún enlace triple, tiene 2 enlaces s y 2 enlaces p (el enlace triple consta de un enlace s y 2 enlaces p). Entonces solo tiene que hibridizar 2 orbitales que son uno s y el otro p, así resulta el orbital sp que es 50% s y 50% p. La geometría resultante es lineal, estando para un lado el enlace simple y para el otro lado el enlace triple formando un ángulo llano (180º). Lo mismo ocurre cuando el carbono forma 2 enlaces dobles, quedando un enlace doble para cada lado, teniendo entonces para cada lado un enlace s y un enlace p. La causa de este tipo de hibridización es que haya 2 enlaces p, sin importar si estén formando un enlace triple o 2 enlaces dobles.

Esta hibridización se da con todos los enlaces triples de los elementos que cumplen con el octeto dado que todos tienen 2 enlaces p. Por ejemplo el nitrógeno tiene CEE = 2s² 2p³ en su estado fundamental. El N₂ utilizará 2 electrones p para formar cada uno un enlace p, restando entonces 2 electrones s y un electrón p. Uno de esos electrones formará un enlace s y los otros 2 formarán el par de electrones libres, así que tenemos un orbital s y un orbital p que se van a hibridizar, dando como resultado sp.

También ocurre con algunos enlaces simples de algunos elementos que no cumplen con el octeto, por ejemplo: el berilio tiene CEE = 2s² en su estado fundamental y CEE = 2s¹ 2p¹ en su estado excitado, entonces tiene 1 electron s y 1 electron p, que se hibridizan de forma sp dando cada uno un enlace simple, por ejemplo BeCl₂, que es estable debido a su geometría lineal.

Regla de las diagonales

Máxima cantidad de electrones por nivel = 2n²; siendo n = Nº de nivel

Por lo tanto:

nivel 1 = 2.1² = 2 electrones

Se ubican en un subnivel s, de forma circular

Así que en el nivel 1 tenemos 1s²

nivel 2 = 2.2² = 2.4 = 8 electrones

Tiene un subnivel s con 2 electrones.

Los demás se ubican en el subnivel p, cuyas órbitas tienen forma de 8.

El subnivel p consta de 3 órbitas: p_x, p_y y p_z, cada una con 2 electrones.

Así que en el nivel 2 tenemos 2s² 2p⁶

2 + 6 = 8

nivel 3 = 2.3² = 2.9 = 18 electrones

Tiene un subnivel s con 2 electrones y un subnivel p con 6 electrones.

Los demás se ubican en un subnivel d, que tiene forma similar al p pero es más grande.

Así que en el nivel 3 tenemos 3s² 3p⁶ 3d¹⁰

2 + 6 + 10 = 18

nivel 4 = 2.4² = 2.16 = 32 electrones

Tiene un subnivel s con 2 electrones, un subnivel p con 6 electrones y un subnivel d con 10 electrones.

Los demás se ubican en un subnivel f, también con forma similar al p.

Así que en el nivel 4 tenemos 4s² 4p⁶ 4d¹⁰ 4f¹⁴

2 + 6 + 10 + 14 = 32

y así sucesivamente.

Para saber el número de electrones se sigue esta fórmula

q = carga = Nº de protones – Nº de electrones

Si el átomo es neutro:

0 = Nº de protones – Nº de electrones

por lo tanto Nº de protones = Nº de electrones

Si el átomo no es neutro:

Nº de electrones = Nº de protones – q

Los electrones no se distribuyen llenando primero un nivel y después el siguiente, sino que el órden es más irregular. La regla mnemotécnica para recordar el órden de distribución es seguir el orden indicado por las diagonales.

Hay que ubicar una cierta cantidad de electrones para llenar el primer orbital, luego una cierta cantidad de electrones para llenar el segundo, y así sucesivamente (no se pasa al orbital siguiente hasta no haber llenado ese orbital). El último orbital generalmente quedará incompleto, y todos los anteriores siempre deben estar completos.

Los orbitales que correspondan al mayor número de nivel serán los externos. Ejemplo:

Los orbitales que correspondan al mayor número de nivel serán los externos. Ejemplo:

elemento = Bromo

Z = 35

1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d¹⁰ 4p⁵

El orbital 4p queda incompleto, todos los anteriores están completos

CEE = configuración electrónica externa = 4s² 4p⁵

(el 3d¹⁰ es interno, por lo tanto no se incluye en la CEE)

Medidas

fm (femtometro) = 10-15 m	fg (femtogramo) = 10-15 g	fl (femtolitro) = 10-15 l
pm (picómetro) = 10-12 pm	pg (picogramo) = 10-12 pg	pl (picolitro) = 10-12 l
nm (nanómetro) = 10-9 m	ng (nanogramo) = 10-9 g	nl (nanolitro) = 10-9 l
m (micrómetro) = 10-6 m	g (microgramo) = 10-6 g	l (microlitro) = 10-6 l
mm (milímetro) = 10-3 m	mg (miligramo) = 10-3 g	ml (mililitro) = 10-3 l = 1 cm3
cm (centímetro) = 10-2 m	cg (centigramo) = 10-2 g	cl (centiilitro) = 10-2 l
dm (decímetro) = 10-1 m	dg (decigramo) = 10-1 g	dl (decilitro) = 10-1 l
m (metro)	g (gramo)	l (litro) = 1 dm3
dam (decámetro) = 10 m	dag (decagramo) = 10 g	dal (decalitro) = 10 l
hm (hectómetro) = 102 m	hg (hectogramo) = 102 m	hl (hectolitro) = 102 l
km (kilómetro) = 103 m	kg (kilogramo) = 103 g	kl (kilolitro) = 103 l = 1 m3
	tonelada = 103 kg = 106 g

recordar que:

10 ⁿ = un 1 con n ceros

10 ^{– n} = 1/10 ⁿ

^ejemplo:

10³ = 1000 = mil

10^-3 = 1 / 10³ = 1 / 1000 = un milésimo

volumen en mks (metro-kilogramo-segundo)

1 ml = 1 cm³

1 l = 1000 ml = 1000 cm³ = 1000 (1/10 dm)³ = 1000/1000 dm³ = 1 dm³

1 kl = 1000 l = 1000 dm³ = 1000 (1/10 m)³ = 1000/1000 m³ = 1 m³

Guías teóricas de Química CBC

Estructura atómica

Guías resueltas

Ejercicios de Biofísica

Ejercicios de Inorgánica escaneados

Ejercicios de Inorgánica tipeados

Guía de genética del Bachillerato internacional

Guía de genética del colegio

Mitosis y Meiosis

Resumen Respiración

Temas del 1º parcial de Biología (08)

Temas del 2º parcial de Biología (o8)